この記事は 4 分で読めます
【ビジネス向け】主成分分析とは|目的や活用方法、具体例を紹介

主成分分析は、回帰や分類といったデータ分析をより効率よく、分かりやすく行うために便利な解析手法で、これを理解すればデータ分析の幅が大きく広がります。
今回は、主成分分析について簡単な原理や目的、活用方法を解説するとともに、特にビジネス面で用いられる具体例を紹介します。
目次
主成分分析とは、多量の説明変数を圧縮して少ない変数でのデータ分析を行うための解析手法
主成分分析とは、データ分析を行う際に多量の説明変数から新しい説明変数を作り、より少ない変数での分析を可能とする解析手法です。マーケティングで顧客分析を行うとき、年齢・性別・家族構成・住所・世帯年収・趣味・嗜好・行動履歴など、大量の説明変数から最適なアプローチを考える必要があります。
説明変数の量が多いとデータの可視化が複雑になるため、分析結果を評価したり、因果関係を追求したりすることが難しくなるほか、変数間に相関があると分析結果が不適切になる可能性が高まります。
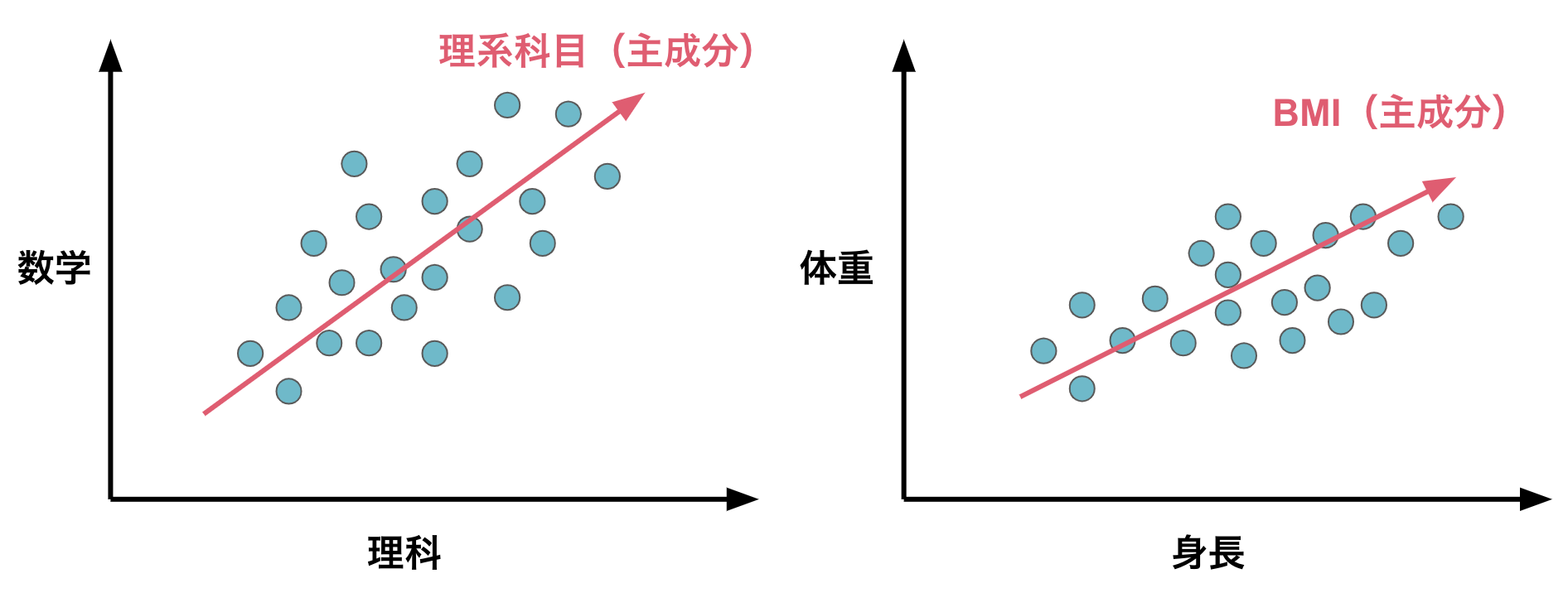
そこで、主成分分析により変数間の相関を用いて情報を圧縮(次元圧縮)し、さらに少ない変数による分析を可能とすることで、これらの困難を緩和します。例えば、テストの総合点と各教科の点数を見るとき、数学と理科の点数には相関があると考えられるため、これらを理系科目と一括りにして分析することで、変数を減らせます。
ほかにも、体重と身長にも相関があるため、これらからBMIという新たな指標を用意し、2つの変数から1つの変数に圧縮するといった例があります。
主成分分析の原理
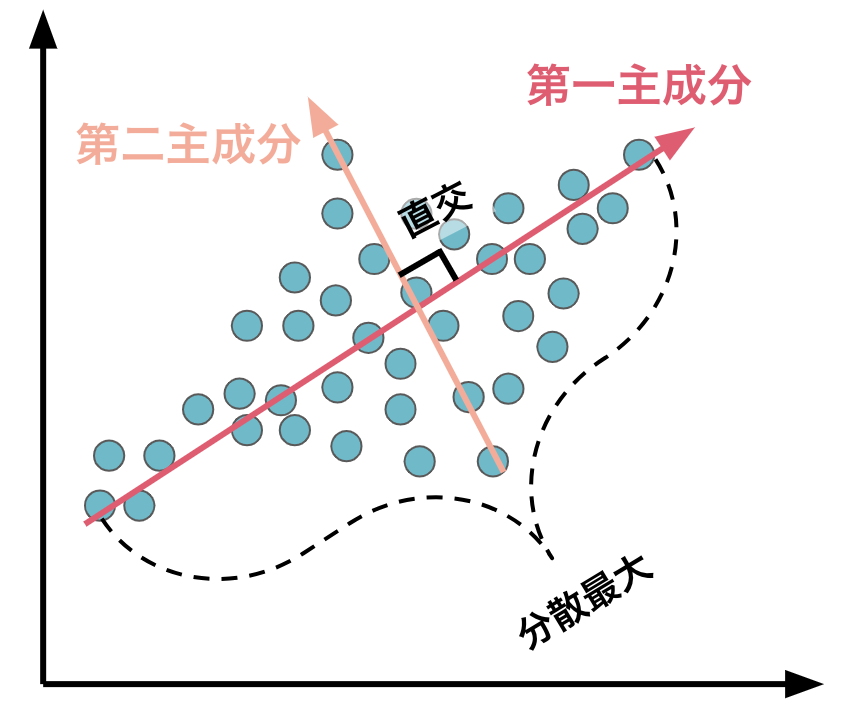
主成分分析の数学的な解釈では、元データの情報量を最大限に確保しつつ次元を圧縮するために、分散(情報量)を最大にするよう第一主成分を決定します。続いて、同様に元データの情報量を最大に確保すべく、分散を最大にするものを主成分に選びます。ただし、第二主成分以降は、これまでと別の情報を得るためにそれまでの主成分と直交する軸を主成分とします。
つまり、第三主成分を決める場合は、その時点で分散が最も大きく、なおかつ第一主成分・第二主成分ともに直交するものを選びます。これを元の変数と同じ回数繰り返す作業が主成分分析です。
主成分の数と元の変数の数は一致しますが、数少ない主成分で元データの多くの情報を保有しており、第一主成分から小さい数字の主成分を使えばよいという意味で次元圧縮と言われます。
主成分分析で重要な言葉
- 固有値
各主成分が、元のデータの情報をどの程度含んでいるかという大きさを示す数値です。固有値が1以上の主成分を分析に使うことが一般的です。 - 寄与率
各主成分が元のデータのうち何%の情報を保有するかを示します。各主成分に含まれる元データの量を固有値よりも直感的にイメージできます。 - 累積寄与率
第一主成分から第i主成分(i=2, 3…)までに含まれる元データの割合を示す数値です。累積寄与率が70〜80%程度に達する程度の主成分を用います。 - 主成分負荷量
元のデータの各変数に与えられる数値で、この値が大きいほど主成分の構成に多く用いられた変数であることを示します。 - 主成分得点
各変数の値(例えば数学のそれぞれの点数)を主成分軸に換算したときの数値を指します。
主成分分析を行う目的
回帰分析における多重共線性を回避する
回帰分析とは、説明変数と目的変数の関係式を導き出す分析手法で、例えば店舗数・商品価格・広告投資費・従業員数といった説明変数を決めた際に、売上という目的変数がどのように変動するかといった予測を行うために用いられます。
特に、説明変数を2つ以上用いる場合を重回帰分析と呼び、重回帰分析を行うときに説明変数同士に相関があると多重共線性が生じ、予測結果が不適切になる可能性があります。
主成分分析を実施してから、主成分で回帰分析を行うことで、変数同士の相関が少なくなり多重共線性を回避できるというメリットがあります。
重回帰分析について詳しくは、以下の記事をご覧ください。
グラフでの可視化を容易にする
通常、3つ以上の説明変数と1つの目的変数がある場合、これらの関係を2次元グラフで可視化することはできません。そのため、グラフを作成する際は自身で1つもしくは2つの説明変数を抽出する必要があります。
主成分分析を実施すれば、第一主成分と第二主成分で元のデータの多くを表現することができるため、散布図などを用いてグラフの可視化が可能になります。
主成分分析の活用方法
1. 全ての変数について主成分分析を行う
説明変数が多すぎて扱いづらい、説明変数同士に相関がありそう、と感じる場合にはまず主成分分析を行うことが効果的です。PythonやRのライブラリを用いることも可能ですが、JMPやSPSS、MATLABといった統計ソフトを用いれば容易に主成分分析を実行できます。
主成分分析では変数を減らしすぎることによりデータを損ない、かえって予測がうまくいかないという現象もあります。そのため適宜、主成分分析の必要性を考えることが重要です。
2. 第一主成分から順に十分な元データを説明できるまで主成分を選ぶ
主成分分析の後、第一主成分からどこまでの主成分を用いて分析するかを決定します。元のデータを十分に保有することが重要で、累積寄与率が70〜80%程度の主成分まで抽出することが一般的とされています。
3. 選んだ主成分を用いて回帰や分類などの分析を行う
続いて、選んだ主成分を用いて、回帰分析による因子分析や将来予測を実施したり、分類により顧客層を特定したりします。主成分分析は、あくまでこのフェーズのためのデータの下準備と考えるとよいでしょう。
4. 分析結果の妥当性と、各主成分が表す元の変数を検証する
分析結果について、経験やドメイン知識をもとに、その妥当性を検証します。同時に、各主成分が元の変数のうち何から構成されたものかを確認し、因果関係を追求できるようにします。
予測結果などが悪ければ、抽出する主成分の量を変えたり、そもそも主成分分析を行わずに相関の強い変数を自分で減らして再度分析したりします。
主成分分析の具体例
アンケート調査の分析
アンケート調査で商品を購入した顧客の声から、どのような顧客層が購入する可能性が高いか、どのようなマーケティングアプローチが適しているかを予測するための準備として主成分分析が用いられます。各質問を変数と見て、主成分分析によって変数を減らし、回帰や分類などの分析を実施して最適なマーケティング施策を考えます。
主成分と元の変数の関係から、どの要素が購買意思の決定に大きく影響を与えているかを分析し、それがなぜかという理由を追求することが、効果的な施策立案の再現性を高めます。
不良品の原因探索
製造現場で不良品が生じた際に、どのプロセスが原因かを見つけることは困難です。特に、大規模な工場の場合、製造工程が複雑であるために操作変数や設備不具合など、原因の可能性が多岐に渡ります。そこで、良品と不良品が作られた際の製造状況から、どの変数に違いがあるかを統計的に分析する方法が注目されています。
製造現場の大量の変数を扱いやすくするため、まず主成分分析を実施するという形態が多いです。
AIによる画像処理
画像処理では画像の各ピクセルごとにデータがあるため、変数が非常に多くなってしまい、AIに学習させる際に膨大な時間がかかってしまいます。そこで、主成分分析を通して変数を大きく減らし、より短時間でAIが学習できるよう工夫するといった方法が挙げられます。



改善の打ち手が見つかる営業の分析手法8選
無料でダウンロードするために
以下のフォーム項目にご入力くださいませ。