この記事は 4 分で読めます
【計算不要】エクセルを利用して重回帰分析を簡単に行う方法を解説

デジタル技術が発展を続ける昨今、ビッグデータ活用の重要性が増しています。特に、データ間の相関を見る回帰分析が、企業活動の計画立案には欠かせません。しかし、統計学や数式の知識を必要とするため、実施するハードルが高いと感じる方も多いと思います。
そこで本記事では、原理や計算方法の知識がなくてもできる、重回帰分析のエクセルでの実施方法を解説します。
※本記事の解説では2019年版のエクセルを使用しています。 メニューの表示箇所や表示形式が若干異なる場合がありますが、バージョンの違いによるものなので、類似のメニューがないか探してみてください。
目次
回帰分析とは、求めたい要素の値が、他の要素の値にどの程度影響されているかを調べる統計学の手法
重回帰分析は、データ間の相関関係を分析する手法である回帰分析の一つです。回帰分析は、値を求めたい要素があるとき、他の要素の値がどれほど影響しているか、つまり相関関係を計算します。
例えば、スタジアムの売上に他の要素がどれほど影響しているか求めたい場合を考えます。まずは複数のスタジアムの売上と、それぞれの最寄り駅からの距離、人口、ファンクラブの人数、広告費など他の要素のデータを集めます。そしてこのデータを基に回帰分析を行うことで、それぞれの要素がどの程度スタジアムの売上に影響しているかという相関関係を求めることができるのです。
重回帰分析についてのより詳しい説明や計算方法などは、以下の記事もご参照ください。
目的変数と説明変数
ここで回帰分析の説明に必要な用語について簡単に紹介します。
まず、求めたい要素の値、つまり先の例におけるスタジアムの売上にあたる値を、目的変数と呼びます。次に、目的変数に影響を与える他の要素の値、つまり先の例における最寄り駅からの距離や人口などの値を、説明変数と呼びます。数式においては目的変数はy、説明変数はxで表されます。
そして回帰分析で求めるのは、それぞれの説明変数についている係数です。係数というのは、y=axのような数式におけるaにあたります。目的変数yは係数aと説明変数xの掛け算で求められるため、係数の値が大きい場合、説明変数の値によって目的変数の結果が大きく変わります。つまり、係数の大きさが相関関係の大きさを示しているのです。
単回帰分析と重回帰分析の違い
回帰分析には単回帰分析と重回帰分析の二種類あります。説明変数が一つだけなのが単回帰分析、複数あるのが重回帰分析です。単回帰分析の場合、説明変数が一つのみ、つまり一つの要素の影響のみで計算することになります。一般的に目的変数は複数の要素の影響を受けるため、説明変数が複数ある重回帰分析の方が、より適切な分析結果を出すことができるとされています。
回帰分析を行う目的
回帰分析を行う目的はまず、目的変数の数値を予測することです。例えば新しいスタジアムをどこに建てるか考える場合、既存のスタジアムに対する重回帰分析で、それぞれの説明変数の係数、つまり目的変数への影響度合いが分かるため、建設予定地の説明変数、つまり人口や市街地からの距離を入力すれば、スタジアムの売上を予測することができます。
また、重回帰分析には、影響の大きい説明変数を見つけ出すという目的もあります。係数の大きい説明変数は目的変数への影響が最も大きいとされます。もし広告費の係数が最も大きかった場合、広告費を上げればスタジアムの売上を最も効率よく上げられることになります。
エクセルを利用した重回帰分析の手順
1. 表にデータを入力
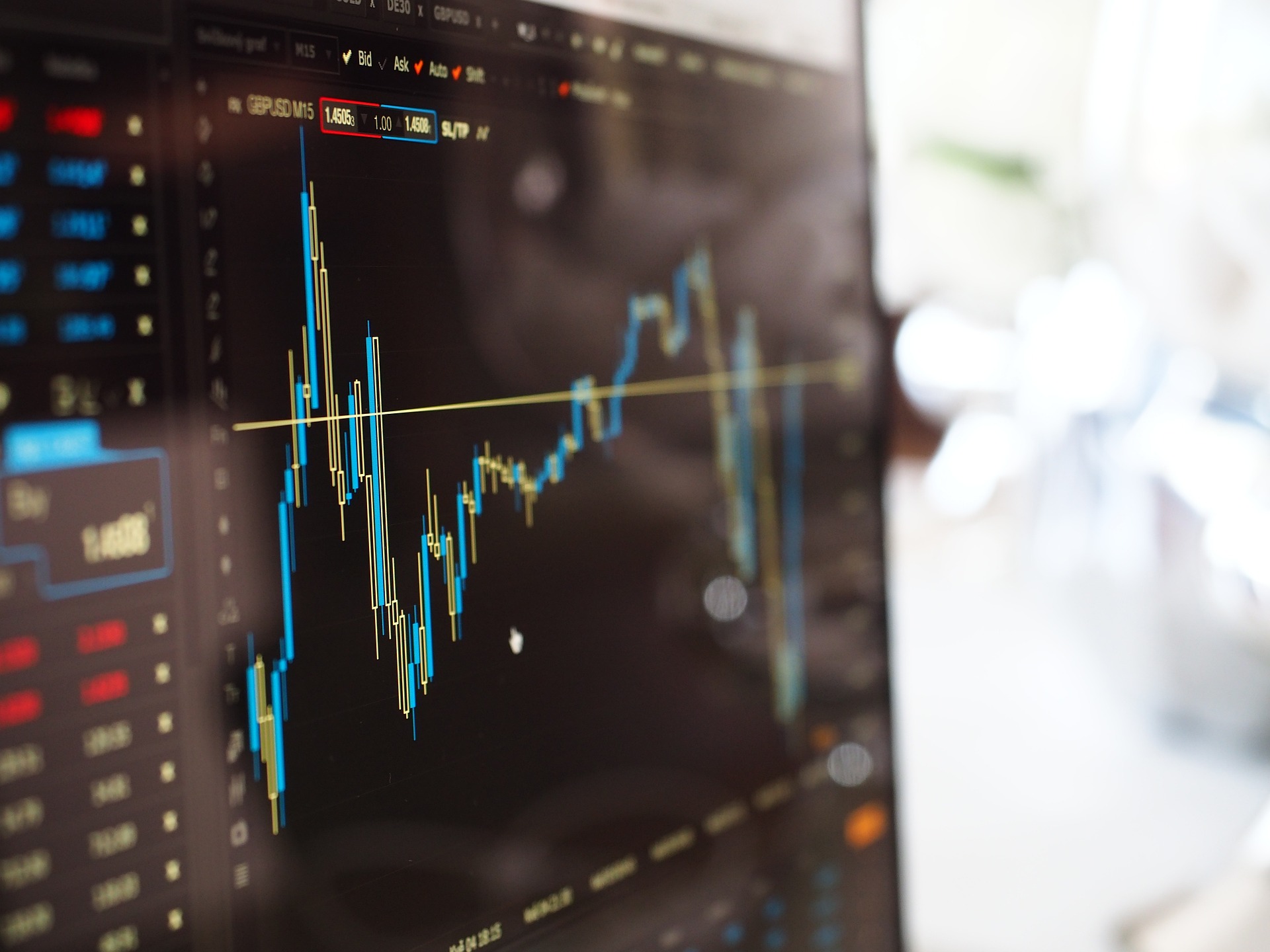
まずは目的変数と説明変数のデータを表に入力していきます。このとき、変数ごとの単位の違いを気にする必要はありません。見やすい形で表を作りましょう。今回は、スタジアムの売上と10km²圏内の人口、最寄駅からの距離、都道府県内の年降水量、所属クラブのファンクラブ人数を表にします。この表の分析では売上が目的変数で、それ以外の項目が説明変数とします。なお、今回は説明のためにデータ数を少なめにしていますが、本来は説明変数の項目数より5倍ほど多く準備した方が、適切な結果が出やすくなります。
2. 「回帰分析」を選択
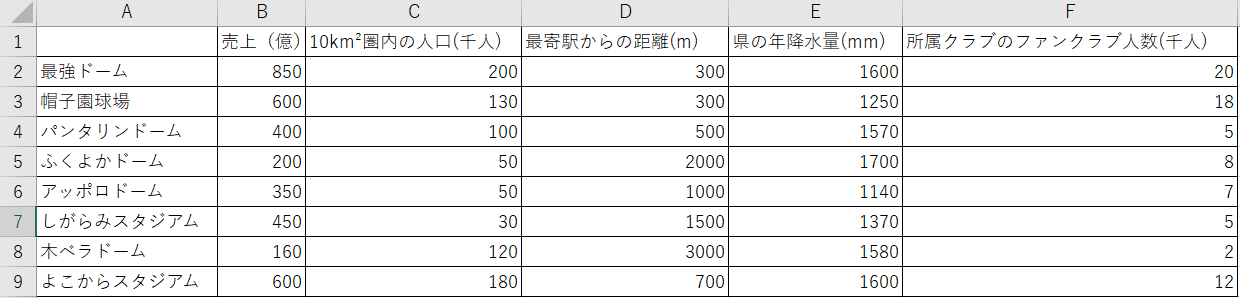
次に「データ」タブから「データ分析」(赤丸の部分)を選択してください。デフォルトでは入っていないこともあるので、その場合は「ファイル」タブから「オプション」ウインドウを開き、「アドイン」タブの「管理」が「Excel アドイン」になっていることを確認したうえで「設定」を開き、「分析ツール」にチェックを入れれば、タブに「データ分析」が現れます。

「データ分析」のウインドウが出たら、「回帰分析」を選択します。
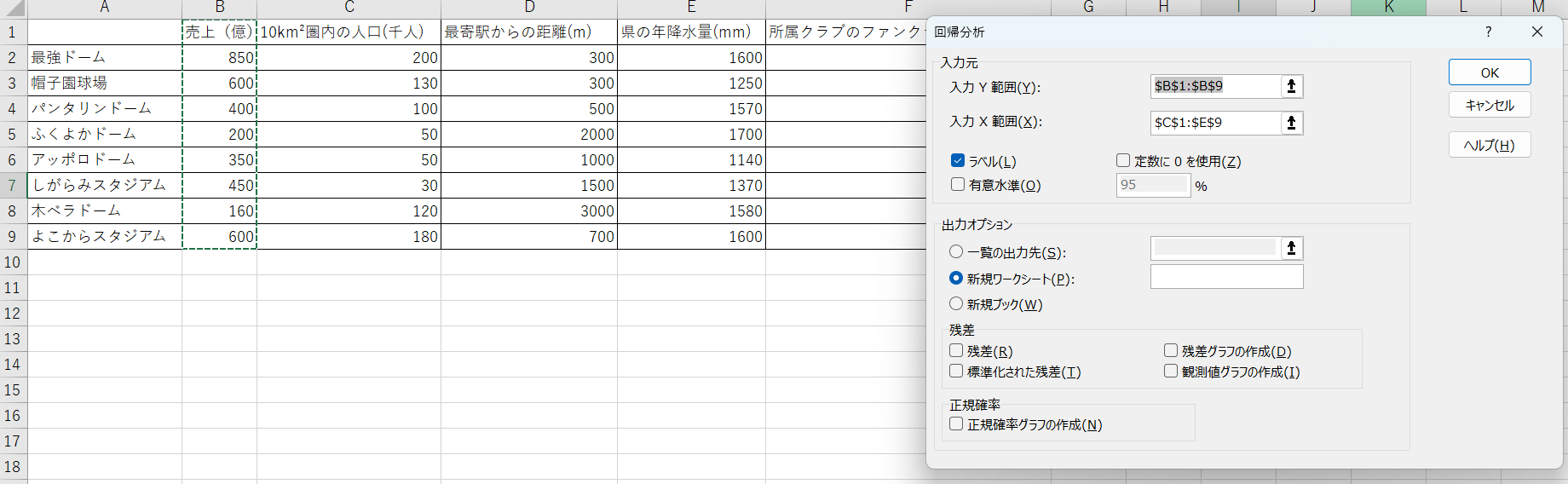
3. 変数となるデータを指定
回帰分析のウインドウが出たら、各値を指定していきます。「入力Y範囲」の項目に目的変数、「入力X範囲」の項目に説明変数となる範囲を指定します。セルの値を書き込む必要はなく、範囲をマウスで指定すれば自動で入力されます。このとき、それぞれの変数のラベル(売上や人口と書かれたセル)も一緒に指定したうえで、「ラベル」のチェックを入れておきましょう。この状態で「OK」を押せば結果が表示されます。
4. 結果を確認
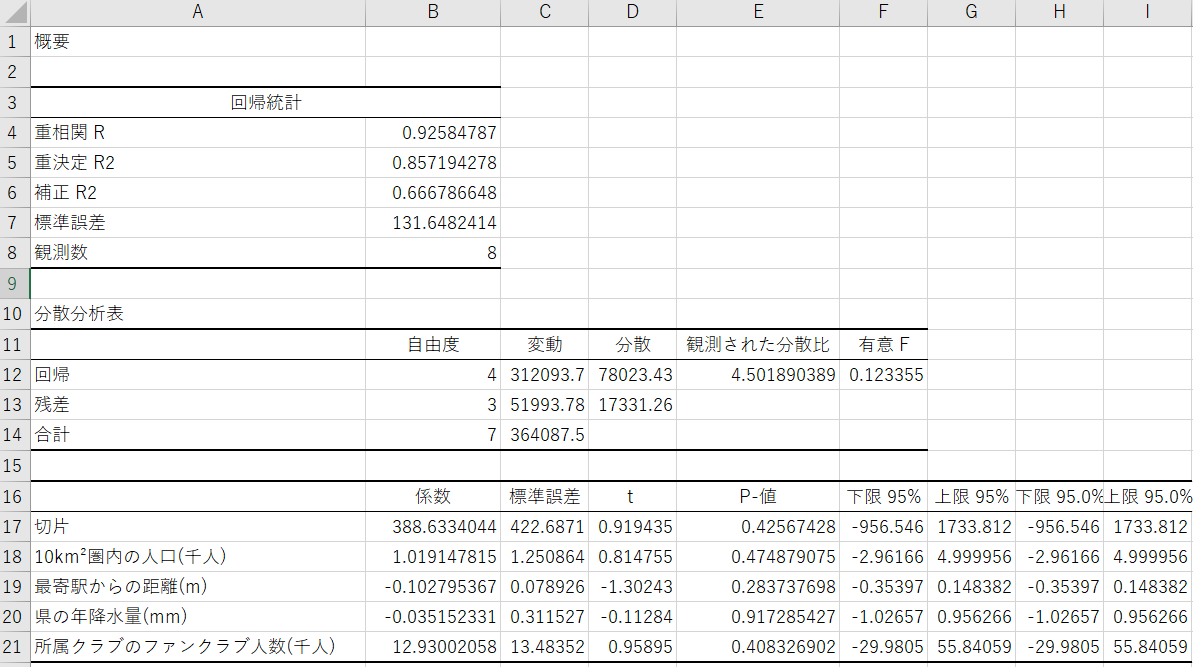
上の表が今回の分析結果の表になります。たくさんの用語と数字が出て分かりづらいですが、分析の目的としては、ひとまず以下の四つの値の意味を知っておけば十分です。
- 補正R2…重決定R2に説明変数の項目数を基にした補正をかけた値です。1に近いほど信頼できる数式であることを示します。
- 有意F…今回の数式が目的変数への影響の説明として適切かどうかを示す値です。0.05以下であれば適切と言えます。
- 係数…それぞれの説明変数につく係数です。数が大きいほど影響が大きいと言えます。切片の係数はそのまま切片の値として使います。
- P-値…それぞれの説明変数が目的変数へ影響している程度を示す値です。0に近いほど目的変数に影響していることを示します。
5. 結果に応じて説明変数を修正する
この説明と表を見比べてみると、今回の重回帰分析は失敗だったことが分かります。説明変数の項目数はわざと少なくしたので、補正R2が低いのは仕方ないとしても、有意Fが0.05に達していないので、今回の数式は目的変数と説明変数の関係を適切に示せていないことになります。
これは目的変数にあまり関係のない説明変数を選んでしまったのが原因ですので、関係のない説明変数を省く、あるいは関係のありそうな説明変数を増やすなどの修正を行います。そこで、P-値を見てみると、年降水量だけ高くなっています。つまり年降水量は目的変数にほぼ影響しないのです。そこで、年降水量を省いてもう一度重回帰分析をやってみます。

補正R2の値はまだ物足りないですが、有意Fの値が0.05を下回ったので、ひとまず適切な関係式を導き出せたことになります。
今回の分析結果を数式にすると、おおよそY=0.95X1-0.1X2+13.2X3+345.8となります。X1は近くの人口、X2は駅からの距離、X3はファンクラブ人数です。このXにそれぞれの値を入れていけば、新しいスタジアムの売り上げも予想できます。
重回帰分析の注意点
重要な説明変数を見逃していないか注意する
回帰分析は、あくまで指定した変数のみから相関関係を出すための手法に過ぎません。そのため、指定しなかった説明変数が持つ目的変数への影響は、指定した説明変数のものと解釈されて計算されます。影響が微小な変数であれば誤差の範囲で済みますが、もし指定しなかった変数の中に影響の大きい要素があった場合、指定した変数が実際以上の影響力を持つものとして分析されてしまうため、計算結果が的外れなものになってしまいます。目的変数の値に影響がありそうな説明変数は、余さず分析に組み込みましょう。
「相関関係=因果関係」ではないことに留意する
回帰分析から分かることは相関関係であり、因果関係ではないことに留意してください。分析結果が示すのは、「ある値が増えたとき、他の値も増えた」ということだけであり、必ずしも「ある値が増えるのは、他の値が原因である」わけではありません。
例えば、「アイスの売り上げが上がる日に熱中症患者が増える」ことは正しいかもしれませんが、どちらも「猛暑」によって増加しているだけであり、二つの要素間に因果関係はありません。
多重共線性を起こさないようにする
重回帰分析は、説明変数の数は7個程度が最も適切であると言われていますが、説明変数を増やす際には多重共線性に気を付ける必要があります。多重共線性とは、説明変数の中に強い相関関係があるものが含まれている状態を指します。
例えば、スタジアムの売上にはその地域の降水量や降水時間が影響しているかもしれませんが、降水量と降水時間には当然強い相関関係があります。この二つを説明変数に含んだまま重回帰分析を行うと、計算結果が的外れなものになってしまいます。説明変数に加える要素は、なるべく互いに独立したもの、つまりそれぞれに相関関係がなく影響し合わないものを選びましょう。



改善の打ち手が見つかる営業の分析手法8選
無料でダウンロードするために
以下のフォーム項目にご入力くださいませ。